Оценка модели машинного обучения

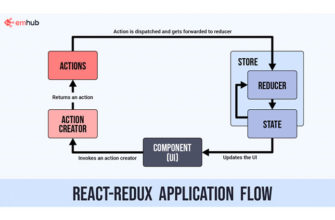
Модель машинного обучения не требует жестко запрограммированных алгоритмов. Мы передаем в модель большой объем данных, и модель пытается самостоятельно определить функции, чтобы делать прогнозы на будущее. Поэтому мы также должны использовать некоторые методы для определения предсказательной силы модели.

Оценка модели машинного обучения

Оценка модели — это процесс, в котором используются некоторые показатели, которые помогают нам анализировать производительность модели. Как мы все знаем, разработка модели — это многоэтапный процесс, и следует постоянно проверять, насколько хорошо модель обобщает будущие прогнозы. Поэтому оценка модели играет жизненно важную роль, чтобы мы могли судить о производительности нашей модели. Оценка также помогает проанализировать ключевые недостатки модели. Существует множество показателей, таких как точность, точность, отзыв, оценка F1, площадь под кривой, матрица путаницы и среднеквадратическая ошибка. Перекрестная проверка — это один из методов, который используется на этапе обучения, а также метод оценки модели.

Перекрестная проверка и задержка

Перекрестная проверка — это метод, при котором мы не используем весь набор данных для обучения. В этом методе некоторая часть набора данных резервируется для тестирования модели. Существует много типов перекрестной проверки, из которых в основном используется перекрестная проверка K-кратности. В K-кратной перекрестной проверке исходный набор данных делится на k подмножеств. Подмножества известны как складки. Это повторяется k раз, где 1 раз используется для целей тестирования. Остальные k-1 складки используются для обучения модели. Таким образом, каждая точка данных действует как испытуемый для модели, а также как субъект обучения. Видно, что этот прием хорошо обобщает модель и снижает частоту ошибок.

Удержание — самый простой подход. Он используется в нейронных сетях, а также во многих классификаторах. В этом методе набор данных делится на обучающий и тестовый наборы данных. Набор данных обычно делится на соотношения, например 70:30 или 80:20. Обычно большой процент данных используется для обучения модели, а небольшая часть набора данных используется для тестирования модели.

Метрики оценки для задачи классификации

В этом коде Python мы импортировали набор данных радужной оболочки, который имеет такие функции, как длина и ширина чашелистиков и лепестков. Целевыми значениями являются Iris setosa, Iris virginica и Iris versicolor. После импорта набора данных мы разделили набор данных на обучающие и тестовые наборы данных в соотношении 80:20. Затем мы вызвали деревья решений и обучили нашу модель. После этого мы выполнили прогноз и рассчитали показатель точности, точность, полноту и показатель f1. Мы также построили матрицу путаницы.

Импорт библиотек и набора данных

Библиотеки Python позволяют нам очень легко обрабатывать данные и выполнять типичные и сложные задачи с помощью одной строки кода.

Pandas— эта библиотека помогает загружать фрейм данных в формате 2D-массива и имеет несколько функций для выполнения задач анализа за один раз.

Numpy— массивы Numpy очень быстрые и могут выполнять большие вычисления за очень короткое время.
Matplotlib/ Seaborn — эта библиотека используется для рисования визуализаций.
Sklearn — этот модуль содержит несколько библиотек с предварительно реализованными функциями для выполнения задач от предварительной обработки данных до разработки и оценки моделей.

Python3

import pandas as pd

import numpy as np

from sklearn import tree

from sklearn import datasets

from sklearn.datasets import load_iris

from sklearn.tree import DecisionTreeClassifier

from sklearn.model_selection import train_test_split

import seaborn as sns

import matplotlib.pyplot as plt

from sklearn.metrics import precision_score,\

recall_score, f1_score, accuracy_score

Теперь давайте загрузим игрушечный набор данных «Цветы ириса» из библиотеки sklearn.datasets, а затем разделим его на обучающую и тестовую части (для оценки модели) в соотношении 80:20.

Python3

iris = load_iris()

X = iris.data

y = iris.target

# Holdout method.Dividing the data into train and test

X_train, X_test,\

    y_train, y_test = train_test_split(X, y,

                                       random_state=20,

                                       test_size=0.20)

Теперь давайте обучим модель классификатора дерева решений на обучающих данных, а затем перейдем к оценочной части модели с использованием других показателей.

Python3

tree = DecisionTreeClassifier()

tree.fit(X_train, y_train)

y_pred = tree.predict(X_test)

Точность

Точность определяется как отношение количества правильных прогнозов к общему количеству прогнозов. Это наиболее фундаментальная метрика, используемая для оценки модели. Формула дается

Accuracy = (TP+TN)/(TP+TN+FP+FN)

Однако точность имеет недостаток. Он не может хорошо работать с несбалансированным набором данных. Предположим, что модель классифицирует, что большая часть данных принадлежит метке основного класса. Это дает более высокую точность. Но в целом модель не может классифицировать по меткам второстепенных классов и имеет низкую производительность.

Python3

print("Accuracy:", accuracy_score(y_test,

y_pred))

Выход:

Точность: 0,93333333333333333

Точность и отзыв

Точность — это отношение истинных срабатываний к сумме истинных срабатываний и ложных срабатываний. Он в основном анализирует положительные прогнозы.

Precision = TP/(TP+FP)

Недостатком Precision является то, что он не учитывает True Negatives и False Negatives.

Отзыв — это отношение истинных положительных результатов к сумме истинных положительных и ложных отрицательных результатов. Он в основном анализирует количество правильных положительных образцов.

Recall = TP/(TP+FN)

Недостатком Recall является то, что он часто приводит к более высокому уровню ложных срабатываний.

Python3

print("Precision:", precision_score(y_test,

                                    y_pred,

                                    average="weighted"))

print('Recall:', recall_score(y_test,

                              y_pred,

                              average="weighted"))

Выход:

Точность: 0,9435897435897436

Напомним: 0,93333333333333333

Оценка F1

Оценка F1 представляет собой гармоническое среднее точности и полноты. Видно, что во время компромисса между точностью и отзывом, если мы увеличиваем точность, отзыв уменьшается, и наоборот. Цель оценки F1 состоит в том, чтобы совместить точность и полноту.

F1 score = (2×Precision×Recall)/(Precision+Recall)

Python3

# calculating f1 score

print('F1 score:', f1_score(y_test, y_pred,

average="weighted"))

Выход:

Счет F1: 0,9327777777777778

Матрица путаницы

Матрица путаницы представляет собой матрицу N x N, где N — количество целевых классов. Он представляет количество фактических результатов и прогнозируемых результатов. Некоторые термины в матрице следующие:

Истинные положительные стороны: он также известен как TP. Это вывод, в котором фактическое и прогнозируемое значения равны YES.
Истинные негативы: он также известен как TN. Это вывод, в котором фактическое и прогнозируемое значения НЕТ.
Ложные срабатывания: он также известен как FP. Это вывод, в котором фактическое значение НЕТ, а прогнозируемое значение — ДА.
Ложноотрицательные результаты: он также известен как FN. Это вывод, в котором фактическое значение равно YES, а прогнозируемое значение — NO.

Python3

confusion_matrix = metrics.confusion_matrix(y_test,

                                            y_pred)

cm_display = metrics.ConfusionMatrixDisplay(

    confusion_matrix=confusion_matrix,

    display_labels=[0, 1, 2])

cm_display.plot()

plt.show()

Выход:

Матрица путаницы для вывода модели

На выходе точность модели составляет 93,33%. Точность составляет приблизительно 0,944, а полнота — 0,933. Оценка F1 составляет примерно 0,933. Наконец, строится матрица путаницы. Здесь метки классов обозначают целевые классы:

0 = Setosa
1 = Versicolor
2 = Virginica

Из матрицы путаницы мы видим, что 8 классов щетинок были предсказаны правильно. 11 тестовых случаев Versicolor также были правильно предсказаны моделью, а 2 тестовых случая virginica были неправильно классифицированы. Напротив, остальные 9 были предсказаны правильно.

Кривая AUC-ROC

AUC (площадь под кривой) — это показатель оценки, который используется для анализа модели классификации при различных пороговых значениях. Кривая рабочих характеристик приемника (ROC) представляет собой вероятностную кривую, используемую для выделения производительности модели. Кривая имеет два параметра:

TPR: это означает истинную положительную скорость. Это в основном следует формуле Recall.
FPR: это означает ложноположительный показатель. Он определяется как отношение ложноположительных результатов к сумме ложноположительных и истинно отрицательных результатов.

Эта кривая полезна, поскольку помогает нам определить способность модели различать разные классы. Давайте проиллюстрируем это с помощью простого примера Python.

Python3

import numpy as np

from sklearn .metrics import roc_auc_score

y_true = [1, 0, 0, 1]

y_pred = [1, 0, 0.9, 0.2]

auc = np.round(roc_auc_score(y_true,

y_pred), 3)

print("Auc", (auc))

Выход:

Аук 0,75

Оценка AUC является полезной метрикой для оценки модели. В основном это подчеркивает способность модели разделять классы. В приведенном выше коде 0,75 — это хороший показатель AUC. Модель считается хорошей, если показатель AUC больше 0,5 и приближается к 1. Плохая модель имеет показатель AUC, равный 0.

Метрики оценки для задачи регрессии

Регрессия используется для определения непрерывных значений. Он в основном используется для нахождения связи между зависимой и независимой переменной. Для классификации мы используем матрицу путаницы, точность, показатель f1 и т. д. Но для регрессионного анализа, поскольку мы прогнозируем числовое значение, оно может отличаться от фактического результата. Поэтому мы рассматриваем расчет ошибки, поскольку он помогает подвести итог, насколько прогноз близок к фактическому значению. Существует множество показателей для оценки регрессионной модели.

В этом коде Python мы реализовали простую модель регрессии, используя CSV-файл погоды в Мумбаи. Этот файл включает день, час, температуру, относительную влажность, скорость ветра и направление ветра. Ссылка на набор данных здесь.

Нас в основном интересует поиск взаимосвязи между температурой и относительной влажностью. Здесь относительная влажность — зависимая переменная, а температура — независимая переменная. Мы выполнили линейную регрессию и использовали показатели для оценки производительности нашей модели. Для расчета метрик мы широко используем библиотеку sklearn.

Python3

# importing the libraries

from sklearn.linear_model import LinearRegression

from sklearn.metrics import mean_absolute_error,\

mean_squared_error, mean_absolute_percentage_error

Теперь давайте загрузим данные во фрейм данных панды, а затем разделим их на обучающую и тестовую части (для оценки модели) в соотношении 80:20.

Python3

df = pd.read_csv('weather.csv')

X = df.iloc[:, 2].values

Y = df.iloc[:, 3].values

X_train, X_test,\

    Y_train, Y_test = train_test_split(X, Y,

                                       test_size=0.20,

                                       random_state=0)

Теперь давайте обучим простую модель линейной регрессии. На обучающих данных мы перейдем к оценочной части модели с использованием разных метрик.

Python3

X_train = X_train.reshape(-1, 1)

X_test = X_test.reshape(-1, 1)

regression = LinearRegression()

regression.fit(X_train, Y_train)

Y_pred = regression.predict(X_test)

Средняя абсолютная ошибка (MAE)

Это простейшая метрика, используемая для анализа потерь по всему набору данных. Как мы все знаем, ошибка в основном представляет собой разницу между прогнозируемыми и фактическими значениями. Поэтому MAE определяется как среднее значение рассчитанных ошибок. Здесь мы вычисляем модуль ошибки, выполняем суммирование и затем делим результат на количество точек данных. Это положительная величина, и направление ее не волнует. Формула MAE определяется выражением

MAE = ∑|y_pred-y_actual| / N

Python3

mae = mean_absolute_error(y_true=Y_test,

y_pred=Y_pred)

print("Mean Absolute Error", mae)

Выход:

Средняя абсолютная ошибка 1,7236295632503873

Среднеквадратическая ошибка (MSE)

Наиболее часто используемой метрикой является среднеквадратическая ошибка или MSE. Это функция, используемая для расчета потерь. Мы находим разницу между предсказанными значениями и истинной переменной, возводим результат в квадрат, а затем находим среднее значение по всему набору данных. MSE всегда положителен, поскольку мы возводим значения в квадрат. Чем меньше MSE, тем лучше производительность нашей модели. Формула МСЭ приведена:

MSE = ∑(y_pred - y_actual)²/ N

Python3

mse = mean_squared_error(y_true=Y_test,

y_pred=Y_pred)

print("Mean Square Error", mse)

Выход:

Среднеквадратическая ошибка 3,9808057060106954

Среднеквадратическая ошибка (RMSE)

RMSE является популярным методом и представляет собой расширенную версию MSE (средняя квадратичная ошибка). Этот метод в основном используется для оценки производительности нашей модели. Он указывает, насколько точки данных разбросаны по лучшей линии. Это стандартное отклонение среднеквадратичной ошибки. Меньшее значение означает, что точка данных находится ближе к линии наилучшего соответствия.

RMSE=√(∑(y_pred- y_actual)²/ N)

Python3

rmse = mean_squared_error(y_true=Y_test,

y_pred=Y_pred,

squared=False)

print("Root Mean Square Error", rmse)

Выход:

Среднеквадратическая ошибка 1,9951956560725306

Средняя абсолютная ошибка в процентах (MAPE)

MAPE в основном используется для выражения ошибки в процентах. Он определяется как разница между фактическим и прогнозируемым значением. Затем ошибка делится на фактическое значение. Затем результаты суммируются, и, наконец, мы вычисляем среднее значение. Чем меньше процент, тем лучше производительность модели. Формула дается

MAPE = ∑((y_pred-y_actual) / y_actual) / N * 100 %

Python3

mape = mean_absolute_percentage_error(Y_test,

                                      Y_pred,

                                      sample_weight=None,

                                      multioutput='uniform_average')

print("Mean Absolute Percentage Error", mape)

Выход:

Средняя абсолютная ошибка в процентах 0,02334408993333347