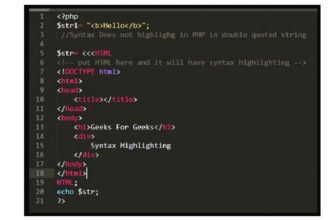
Рекурсивный подход очень подходит для тех задач, которые можно разбить на более мелкие, простые и повторяющиеся задачи. Это процедура, в которой функция вызывает себя многократно/рекурсивно, и должно быть хотя бы одно условие завершения/остановки, чтобы остановить рекурсию. Метод, который вызывает сам себя, описывается как рекурсивная функция, а весь процесс в Java известен как рекурсия.
Что такое рекурсия в Java?
Обычно мы наблюдаем, как функция вызывает какую-то другую функцию или функции. Однако рекурсивная функция многократно вызывает сама себя. Приведенные ниже фрагменты показывают, чем обычный метод отличается от рекурсивного.
Базовый синтаксис нормальной функции
publicvoidfirstFunction()
{
System.out.println(«This is a normal Function»);
secondFunction();
}
Приведенный выше фрагмент показывает, как выглядит обычная определяемая пользователем функция, т. е. она имеет несколько операторов (кода) и вызывает функцию с именем secondFunction().
Базовый синтаксис рекурсивной функции
Теперь давайте посмотрим на приведенный ниже фрагмент, чтобы понять, как выглядит рекурсивная функция:
публичная недействительная первая функция ()
{
System.out.println(«This is a Recursive Function»);
firstFunction ();
}
Рассмотрим приведенный ниже рисунок, чтобы понять, как будет работать приведенная выше рекурсивная функция:

На приведенном выше рисунке показано, что функция постоянно вызывает сама себя, т. е. возникает сценарий бесконечного цикла. Теперь вам должно быть интересно, если функция постоянно вызывает себя, то как она остановится? Хорошо! Мы должны определить критерии завершения, чтобы остановить такую функцию в какой-то момент.
Условия остановки/завершения
На данный момент ясно, что должно быть условие, которое будет управлять потоком рекурсивной функции. С точки зрения программирования условие, которое останавливает вызов самой функции, называется условием остановки или базовым случаем.
Синтаксис рекурсивной функции с условием остановки будет выглядеть примерно так:
public void functionName()
{
functionName();
//termination condition;
}
Состояние остановки может быть любым в зависимости от различных обстоятельств.
Примеры рекурсии Java
Этот раздел предоставит подробное понимание того, как рекурсивная функция работает с базовым случаем в Java.
Пример
Приведенный ниже фрагмент берет число от пользователя и находит факториал этого числа:
publicclassFactorialClass {
staticintfindFactorial(int num) {
if (num == 0) {
return1;
}
else {
return (num * findFactorial(num — 1));
}
}
}
В приведенном выше фрагменте кода условие if-else используется для остановки рекурсии, когда «num» становится равным «0».
publicstaticvoidmain(String[] args) {
Scanner scan = new Scanner(System.in);
System.out.println(«Enter a positive number:»);
int number = scan.nextInt();
if (number <0) {
System.out.println(«You Entered an invalid number:»);
} else {
int result = findFactorial(number);
System.out.println(«Factorial : « + result);
}
}
В основном методе мы получаем число от пользователя, проверяя, является ли число допустимым или нет, и, если число допустимо, вызываем метод findFactorial(). Весь код будет генерировать следующий вывод:

Вывод подтверждает, что рекурсивная функция работает правильно и правильно вычислила факториал 6.
Заключение
В Java процесс, в котором функция вызывает себя снова и снова, называется рекурсивной функцией/методом, а весь процесс известен как рекурсия. Базовый/остановочный случай должен быть определен в рекурсивных функциях, чтобы остановить рекурсию в какой-то момент, иначе функция никогда не остановится и вызовет себя неограниченное количество раз. В этой статье подробно рассматривается, что такое рекурсия, разница между обычной и рекурсивной функциями и как создавать рекурсивные функции в Java.